Rationalist Explanations for War: A Quick-and-Dirty Primer

Leopold, Prince of Hohenzollern, found himself in the middle of quite the bargaining pickle from 1868 to 1870.

Consider this a post as a primer for my upper-division students in international conflict. I’m in the process of revising how I teach this class while my department is also prioritizing who teaches what classes in international relations. I’m expecting to be teaching less of my bread-and-butter intro class and more of my upper-division international conflict course. However, the framework of my revamped upper-division course depends on students having some familiarity with the crisis bargaining framework best elaborated in James Fearon’s (1995) “Rationalist Explanations for War.” My intro kids get heavy doses of this framework early in the semester and get it reinforced through applications throughout the semester. My upper-division class assumes this because I’m usually teaching the intro class as well, but I’ll be doing that less going forward. Further, not every intro-to-IR instructor teaches this framework, eschewing a “rationalist” framework in lieu of other “-isms.” This is fine—I’m not wading into this topic as others have and y’all do you—but I can expect to be getting more students in my upper-division course that have not been introduced to this stuff. So, I’m writing this quick-and-dirty primer so that I can put it on my syllabus and have my students read it in the first week.

Here’s a table of contents.

1. A Perspective Toward the Study of International Relations
2. How Might We Understand Why States Fight Wars From This Perspective?
   • Solving This Simple Model
   • How Else to Wrap Your Head Around This?
3. So Why Does War Happen in This Framework?
   • Issue Indivisibility
   • “Uncertainty”
   • Commitment Problems
4. Conclusion

Before beginning, I want to offer the following caveat about what follows. The intuition behind this framework for understanding war leans on game theory and formal theory, though my upper-division courses tend to eschew formal theory and game theory in favor of a more “EITM”-ish approach to the study of conflict. I’m more interested in the quantitative side of things than the formal-theoretic side of things. The mathematics and game theory elements of what follows are here to formalize this intuition and offer basic proofs of it. A student does not need to internalize the mathematics in order to get the basic takeaways. A student who is interested in unpacking this intuition in more detail should consider reading or watching William Spaniel’s stuff since he is way better at this stuff than I am. I consider what follows as a basic foundation upon which I teach a more “correlates of war” class at the upper-level.

A Perspective Toward the Study of International Relations

Perspectives precede theory, though we don’t often belabor this point to our undergraduates. A perspective is a general orientation toward the world (here: “international relations”, broadly defined). Perspectives are broad—so broad that they’re ultimately untestable. Theories that follow from these perspectives create hypotheses that can be set up for evaluation. However, the perspective is the basis on which we develop whole theories.

In the context in which I teach, the perspective is that the international system is comprised of sovereign states (i.e. “countries”, as the Americans call them) in an anarchic international system.¹ “Anarchy” conjures a lot of imagery, but it minimally means there is no world government akin to the domestic governments of sovereign states (i.e. a-narchy = “without government”). Further, states are contesting issues that are fundamentally scarce (i.e. there is finite availability for, say, land or various natural resources) and rivalrous (i.e. consumption of a good by one state [e.g. land] precludes equal consumption for another state). States that are jockeying for these goods in an anarchic international system are both rational and strategic. Both terms overlap considerably, but are fundamentally different. States are “rational” in that they have transitive preferences (i.e. no “rock-paper-scissors” preference orderings), weigh expected costs and benefits among possible decisions, and choose courses of action that maximize expected utility to the best of their abilities. More importantly, for this perspective, states are “strategic” in that they must anticipate how the decisions they make will result in a response from another state that is also competing for the same issue. If, for example, an offense in (American) football is trying to establish its run game, it can expect the strategic response from the opposing defense is to bring a safety in the box. This is typically when the offense hits the defense with a play-action pass. Likewise, China can expect that its increasing naval presence in the South China Sea is going to warrant a militarized response from the Philippines. Whether that’s enough to deter China (it’s not) is another matter, but Chinese decision-makers are making strategic calculations about its presence in the South China Sea expecting (among other things) how the Philippines will respond.

Thus, a perspective toward the world under observation that emerges is a case where 1) states (but see first footnote) are the fundamental unit of analysis that are 2) operating in an anarchic international system while 3) competing for scarce/rivalrous goods with other states and 4) needing to condition their behavior to maximize their chances of getting what they want while acknowledging that choices have consequences constituted as reprisals from other states that want the same goods. This may not mesh with what an intro class may have taught them, but it does inform how I teach students at both the intro-level and upper-level.

How Might We Understand Why States Fight Wars From This Perspective?

Why states fight wars with each other is perhaps the oldest and most important question in the whole field.² This perspective assumes that how states interact with each other over a contentious issue (e.g. land) in an anarchic international system is a form of a bargaining interaction. In other words, states interact with each other in a manner not at all dissimilar to how a buyer and a seller haggle over a good in a bazaar or how a star athlete will hold out for a new contract from the franchise owner. There is one wrinkle, though. When bargaining “fails” in the context of a haggling situation or a wage/raise situation, the outcome is not terribly climactic. A haggling situation that fails means the buyer and seller could not agree on a price of some good in the bazaar and that there is no transaction. When bargaining “fails” in the context of a wage dispute between a star athlete and franchise owner—or any employer-employee context—the end result is typically the employee leaving for another opportunity.

When bargaining “fails” in this context, there’s a war between two disputants. Why they fight the war is what we want to understand and the framework for answering that question treats war as akin to “bargaining failure” in which states fail to peacefully resolve some issue.

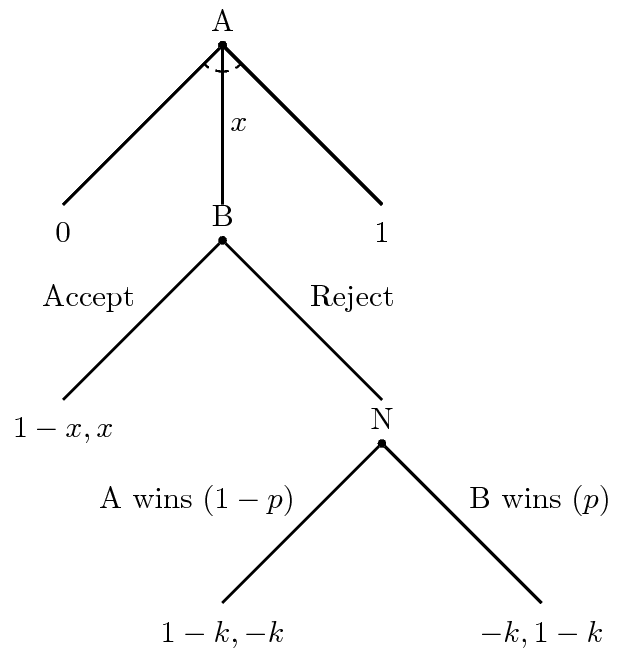
Let’s set up an illustration of what this resembles. This illustration is going to be heavily stylized and super simple. It is not supposed to be a realistic model of all forms of conflict between states, only a useful illustration that gets at the core of the problem. In this simple setup, there are just two states—we’ll call them State A and State B. There is some contentious issue they’re trying to settle. You can think of this as dividing territory, determining how open State B should be to State A’s goods, or really anything else. There is also just one basic interaction each in this simple game. State A is going to make a take-it-or-leave-it offer to State B. If State B accepts, the good in question is divided peacefully and there is no war. If State B rejects, State A and State B will fight a war. Think of this as a crisis bargaining situation. Two states are at the brink of war and only accepting a take-it-or-leave-it offer will avoid it.

Let’s set this up a little more formally as an extensive form game (i.e. decisions are made sequentially and not simultaneously). This graph does not appear in Fearon’s (1995) article but it’s a way of representing what he’s describing. No matter, consider this graph below with some explanation afterward.

A Simple Crisis Bargaining Model

Here, State A starts the game by making a division of the disputed good in question. The good itself—whatever it exactly you want to think of it as—is standardized to be between 0 and 1 and State A will make a division of it and offer it to B. This offer is \(x\). If \(x\) is 0, that is A’s way of telling B that B is not getting anything and A is going to take everything. If \(x\) is 1, State A is offering to give State B the entire good in question. If it helps, you can think of an offer like \(x = .65\) as equivalent to saying State A is going to offer State B 65% of the good in question while State A will keep the remaining 35%. This is a bit more intuitive in, say, a land dispute but it has broad applicability elsewhere. Indeed, the JCPOA between Iran and the P5+1 comes with a recognition that there is some \(x\) of the good of Iranian uranium enrichment that is palatable to the P5+1. Above that threshold, Iran could accelerate a nuclear weapons program (unacceptable to the P5+1). Below that threshold, Iran is using uranium enrichment for its domestic energy industry and could not conceivably develop such a weapons program in the near future (acceptable to the P5+1).

State B only moves in this game after State A has made an offer. If State B accepts the offer, the game ends without a war. State B will receive the offer of \(x\) and State A will receive the remainder of the good in question (\(1-x\), where \(x + 1 - x = 1\) [the full good in question]). If State B rejects the offer, there is a war whose outcome is determined by Nature (N). Capital-N Nature only moves in this game if State B rejects State A’s demand. In this context, Nature has no stake in this situation. It does not favor A or B. Instead, Nature is a preference-less robotic actor that assigns outcomes based on probability. Here, Nature is saying there is some set probability (\(p\)) that B wins the war and some other probability that A wins the war (\(1 - p\)). This is a simple case; the war is going to have a winner (i.e. no stalemates) and the probabilities equal the full domain of the outcome space (i.e. \(p + 1 - p = 1\)). If B wins the war, B will take the full value of the good in question (1) and A will get none of the good in question (0). Likewise, A winning the war means A will take the full value of the good in question (1) and B will get none of it as a punishment (if you will) for having the gall to reject A’s offer. Nature is simply saying either outcome is probabilistic. B wins with probability \(p\); A wins with probability \(1-p\).

However, there is a cost to war for both sides that is 1) positive and 2) subtracted from the utility of getting the good in question. This will be a simple case; the cost for the war is \(k\) for both sides (win or lose).³ It also helps (but is not necessary) to think of \(k\) as a proportion (e.g. \(k = .3\) could be equivalent to saying the war was 30% of a state’s entire national capacity). No matter, \(k\) is subtracted from the payout, win or lose. It is the cost of fighting the war that cannot be recouped. Thus, if A wins the war, A’s payout is \(1 - k\) and not simply the 1.

Solving This Simple Model

A student who wants to unpack/solve this model will need to engage in a process called “backward induction.” This is a fancy way of saying that understanding how strategic actors play games ex ante requires starting at the end of the game and working back to the beginning. That means starting with Nature. Nature moves last in this game—if it moves at all—because its “move” depends on B rejecting A’s offer (which in turn depends on the offer of \(x\) that A makes).

Mercifully, this is a simple solution, albeit not one that students enjoy if they thought there would be no math in political science. Nature has no skin in this game. It has no vested interest in A or B. It’s equivalent to a pull of the lever, simply saying there is some objective probability of victory in war for both sides and simulating what would happen if B rejected A’s demand. Thus, A and B do not have to anticipate what Nature will do, per se. It has to understand that “Nature” is saying there is some probability of one payout and another probability of another payout for the war. Alternatively: Nature is saying that A and B need to calculate the expected utility for war.

We’ll start with A here. If there’s a war, A is winning with some probability \(1 - p\) and losing with some probability \(p\). If it wins, the payout is \(1 - k\). If it loses, the payout is \(-k\) (or, \(0 - k\) in which the zero drops out for convenience). One outcome for A is clearly preferable to the other, but the value that A associates with it needs to be weighted by the probability of actually getting it.⁴ This is the expected utility part of the equation.

A student who remembers the FOIL method from high school should be fine here. The expected utility of war for A is equal to \((1 - p)(1 - k) + p(-k)\). The FOIL method decomposes this to \(1 - k - p + pk - pk\). Moving stuff around/cancelling stuff out on top of that produces an expected utility of war for A that is \(1 - p - k\). The benefit of standardizing the payout of the good in question is that it provides a convenient interpretation of this expected utility of war for A. Conceptually, the expected utility of war for A is equal to its probability of victory (\(1 - p\)) weighting the full value of the good in question (1, which drops out for shorthand), minus the cost of war (\(k\)) that it pays no matter what.

We have to do the same for B as well.

B’s expected utility for war is equal to \((1 - p)(-k) + p(1 - k)\), which decomposes to \(-k + pk + p - pk\). Canceling out and moving stuff around on top of that produces a final expected utility of \(p - k\). Conceptually, the interpretation is analogous for B as it was for A. The expected utility of war for B is equal to its probability of victory \(p\) weighting the full value of the good in question (1, which drops out for shorthand), minus the cost of war (\(k\)) that it pays no matter what.

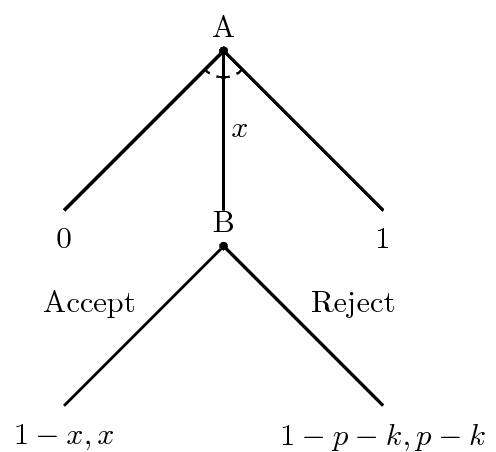
We have successfully removed Nature from this game, resulting in a simplified version of the game below.

A Simple Crisis Bargaining Model (with Nature Removed)

We continue the backward induction process now with B. B ends the game no matter what happens next, at least in terms of this simplified game that reduces the outcome of the war to expected utilities. If B accepts the offer of \(x\), it gets \(x\). If it rejects the offer, it will fight a war that it might win or lose but calculates the expected payout to be \(p - k\). Thus, understanding what B will do here is fairly straightforward. Assume, reasonably, that both sides are risk-averse and will accept a deal that at least equals their expected payout from war, then B will accept a deal where \(x \ge p - k\). B will reject the deal (and there will be a war) when \(x < p - k\). B doesn’t need to look ahead at this point. It’s abstracted the logistics of the war and assessed its expected value for waging it. It’s just simply weighing what it likes more: the offer or the war.

Put in other words, we say an offer of \(x\) that at least equals B’s expected utility for war (\(p - k\)) is a minimal one that B would accept. Would A offer that, though? If B would accept an offer of \(x\), then A would get \(1 - x\). For it to be worth A’s time to offer \(x\) to B to avoid the war, the payout it gets from the deal must be greater than A’s expected utility of the war. More formally, for B to accept \(x = p - k\), it must also be true that \(1 - x \ge 1 - p - k\). More informally, B will fight if it’s getting lowballed and A won’t offer if B’s demanding too much in terms of \(x\).

The big question here is if \(x = p - k\) and \(1 - x \ge 1 - p - k\) are both true. The answer here is yes and the implications are multiple. Recall that we assumed that the costs of war are positive and are subtracted from the payout of war for both sides (win or lose). From that, we can say \(1 - x \ge 1 - p - k\) by definition. Observe:

Where \(k > 0\) and \(p\) follows the rules of probability, it is also the case that \(p + k \ge p - k\) by definition. There exists, conceptually, a range of possible deals that A would offer and B would accept. Consider the graph below as illustrative.

A Conceptual Bargaining Space

Observe the continuum between 0 (A’s ideal point) and 1 (B’s ideal point). Where \(p - k > x\), the offer on the table is much closer to A’s ideal point and too far from B’s ideal point and what B is willing to accept. In this situation, A is lowballing B and B prefers war to the offer on the table. When \(x > p + k\), B is being too demanding. What B is demanding from A in terms of \(x\) is too far from A’s ideal point (if close to B’s ideal point). B would clearly take this offer of \(x\). However, A wouldn’t offer it because it’s payout from the deal (\(1 - x\)) is less than its expected utility for war.

Here, it’s worth noting for students that there is an equilibrium outcome of this game. A has a first-mover advantage and everything is common knowledge. Both A and B know and agree on the parameters of the game. B, however, does not get a counteroffer. This means the offer that gets made is the bare minimum that B would accept (\(x = p - k\)). A would not offer anymore than that because it is not necessary for B to accept and would only diminish its own payout from this bargaining interaction. Don’t misunderstand; A wants to avoid a war with B. It doesn’t care to be too nice to it.

How Else to Wrap Your Head Around This?

I like to give students some applications of what this model is communicating. One is kind of silly. Another is a bit more substantive, albeit with a caveat.

Assume a hypothetical situation where a student is with their friend walking down an off-campus alley in which they encounter a $100 bill. Both players in this game—Student and Friend—want all the $100 because $100 is a lot of scratch for a college student who wants to buy textbooks or, better yet, wants to go HAM on all-you-can-eat-wings night. So how might they settle this issue? One path forward here is a nod to one of my all-time favorite fantastically terrible movies: Bloodsport.⁵ Perhaps they can set up a pit for a fight for the low-low price of $20. First one to say “matté” (i.e. tap out, a la Bloodsport) loses. Winner gets the $100 purse. Assume, for simplicity’s sake, Student and Friend are evenly matched (\(p = .5\)). That means the expected utility for Kumite is $30 for both sides (i.e. \((100)(.5) + (0)(.5) - 20 = 30\)). By itself, this is a fantastic lottery (i.e. for $20, either Student or Friend wins $30 on average). However, if Student offers Friend $30, and Friend is not permitted a counteroffer, then both could divide the $100 and avoid combat. Ultimately, any deal between $30 and $70 is sufficient for a deal, though Student has the first-mover advantage and takes home $70.

The more substantive interpretation is this ultimatum game does well to capture the July Crisis, however you want to stylize it. In this context, the Austrian government used the assassination of an unpopular Austrian archduke as pretense for an ambitious ultimatum to Serbia that would amount to a near total concession of sovereignty. Austria demanded total acceptance of all terms. Serbia hedged on one part of it—about allowing Austrian officials to police subversive, anti-Austrian elements in Serbian territory—which was enough to equal a rejection of the terms. Austria declared war on Serbia. The conflict ballooned from there. Again, this is stylized, and Wagner (2000) would add that war is politics by other means and more wars look like the Russo-Japanese War than World War I.⁶ No matter, this crisis bargaining model is insightful for this application. Those interested in way better game-theoretic interpretations of World War I should buy Scott Wolford’s book on the matter.

So Why Does War Happen in This Framework?

No matter how informative, this model seems to suggest war should never happen (at least as I have set it up so far). Conceptually, an \(x\) exists between \(p - k\) and \(p + k\) and that implies A and B should always find it even if the outcome of the model might be more advantageous to the state making the offer. However, war still happens no matter how rare the event is. This framework leads to three broad classes for why bargaining fails and states fight wars. These are 1) issue indivisibility, 2) “uncertainty”, and 3) credible commitment problems inherent to an anarchic international system.

Issue Indivisibility

This is usually the most intuitive thing for beginners to understand, but it also happens to be the least interesting or useful explanation in this framework. An implicit assumption in the model that I did not belabor is that the good in question is infinitely divisible. \(x\) can be .5, .501, .50000001, or anything else between 0 and 1. State A could cede 30% (\(x = .3\)) of some piece of territory to State B, or eliminate tariffs on 30% of State B’s goods, or anything to that effect. However, sometimes the good cannot be divided. One side is getting all of the good or none of the good. Under those conditions, bargaining failure is a fait accompli.

There are several examples that are consistent with this. For example, students learn in my intro class (and learn again in my upper-division class) that the allocation of territory a core cause of violent conflict in the international system. More wars are contested over the allocation of territory than any other issue. This is because the benefits of contested territory typically accrue only to the side that occupies and controls it, whether the territory’s value is tangible or symbolic. There is no division that is ultimately palatable to either side under those conditions. One side is getting everything or nothing. Deadly conflict observed in places as diverse as Kashmir and the West Bank would be consistent with this.

There is also a particularly intriguing (if stylized) case of issue indivisbility coinciding with war. This concerns the deposition of Queen Isabella II of Spain after an 1868 revolution. The new government that overthrew Isabella II offered the Spanish crown to Leopold of Hohenzollern. This offer from the new Spanish government, combined with Otto von Bismarck’s tongue-in-cheek endorsement of the offer, was a complete non-starter for Napoleon III of France. Spain was a predominantly Catholic country under considerable French influence at the time. This candidate for King of Spain was a Protestant and ethnic German from the same royal dynasty that controlled the Kingdom of Prussia. There was no way France would permit the new Spanish king to be a German, let alone a relative of the Prussian king. Under those conditions, how does the issue resolve in this framework? Is Leopold king of Spain three days a week and the French candidate king for another three days a week with alternating Sundays? This setup is rather foreign in the world of monarchical succession. The fallout from this ultimately led to the Franco-Prussian War that unified the German states into the single “Germany” that we (mostly) still have today. The issue could not be resolved without a war.⁷

That said, scholars like to discourage people from putting too much stock into this class of bargaining failure. It is only nominally a reason for bargaining failure. Territory—that one issue that seems effectively indivisible—is that one thing people have been dividing for centuries. They’re called “borders.” If an issue like territory seems “indivisible”, it’s more important to explore how leaders framed an issue toward that end. Further, issue indivisibility can become a different problem to be mentioned later—a commitment problem—as a result of “side payments.” Consider the 1898 Treaty of Paris, in which the United States successfully dissuaded Spain from restaking its claim to the Philippines after cutting the Spanish crown a check for $20 million. The United States did not divide the Philippines with the Spanish; it took the island and bought them off after the fact with a side payment. So, yes, issue indivisibility is a reason for bargaining failure, but it’s not a very compelling reason for thinking about war.

“Uncertainty”

There are any number ways of unpacking this reason for bargaining failure. Here, students might get more sophisticated discussions of incomplete information and imperfect information. There are also issues here of information asymmetry. However, it’s adequate for the cause of this primer to think of this as general “uncertainty” about the nature of the game. Applied more formally to this simple crisis bargaining model, we assumed \(p\) and \(k\) were common knowledge to State A and State B. In the real world, however, few things are common knowledge and both State A and State B have every incentive to misrepresent their capabilities when they bargain over a contentious issue. Don’t misunderstand; we assume states in this model prefer to avoid the war. They also want to do as well as they can in any deal reached. Toward that end, states bluff and misrepresent their capabilities. This makes bargaining more difficult and invites bargaining failure.

Let’s apply this to the bargaining game with a simple illustration, one that does reasonably well highlighting the basic problems of the American military in several of its wars after World War II. Let’s assume State A (the United States, if you will) has a major conventional military advantage and its assessments of its military advantage lead to internal optimism about what the war would look like for State A. State A assumes its own probability of victory in war is .8 (i.e. \(1 - p = .8\)). That would mean State A believes B’s probability of victory is .2. Let’s standardize \(k\) here to be .1. If A believes this is the nature of the game, the greatest \(x\) with which it is willing to part is .3 (i.e. \(p + k = .2 + .1 = .3\)) and the possible range of \(x\)s is anything between .1 and .3.

However, State B does not share State A’s assessment about the nature of what the war would resemble. State B concedes A’s major conventional military advantage and instead fights more asymmetric conflicts in which conventional militaries molded from great power wars have traditionally struggled. State B believes \(p\) is .5, and we’ll hold constant the \(k\) here to be .1 as well. Under those conditions, the minimum \(x\) that B would accept from A is .4 (i.e. \(p - k = .5 - .1 = .4\)). So, notice what happens here. The maximum A would offer is .3. The minimum B would accept is .4. Both sides see more utility in fighting because uncertainty about the nature of the game (just \(p\) here) erases all possible values of \(x\) to which both sides could agree.

Generally, I think this class of reasons for bargaining failure does well to get at why war minimally starts. However, it does less well explaining why some wars drag on forever and why some wars recur. The Iran-Iraq War lasted eight years and is one of the longest inter-state confrontations in the post-Napoleonic history of the world. The Russo-Japanese War, by contrast, lasted a little over a year and ended when successive battles revealed to the Russians that they were nowhere near as equipped to defend its position in the Korean peninsula as they thought at the onset of the war. Shouldn’t the Iranians and Iraqis have learned that a year or two into their war and negotiated a stalemate? Further, war is not a random event. India and Pakistan were effectively born into war and have fought four total since 1947. They’ve had 20 total fatal confrontations in that same time frame. An identical assessment holds for the Israel-Syria dyad. Both are No. 1 and No. 2 for the most conflict-prone dyadic pairings after World War II.⁸ Understanding situations like this leads to understanding commitment issues endemic to an anarchic international system.

Commitment Problems

This framework puts less emphasis on the anarchic nature of the international system than the “-isms”, but it is still an important backdrop toward understanding the causes of war. Namely, the anarchic international system means little exists to ensure negotiated settlements hold and there is no certainty that both sides are ultimately negotiating in good faith. Commitment problems abound in international relations, but two are worth considering in some detail.

First-strike advantages are real problems in inter-state crisis bargaining and were effectively abstracted out of the simple crisis bargaining game above. That game modeled the war almost as if it were a boxing contest. B rejects A’s demand and Nature rings a bell, starting a fight. However, IR’s defining feature in its approach to bargaining interactions is that states can use violence as bargaining tools. Let’s apply this to the bargaining model above. Assume B has a possible first-strike advantage, such that:

Informally, B’s probability of victory in war if it sucker-punches A first is greater than its probability of victory in war if they both attack simultaneously. This, in turn, is greater than its probability of victory in war if B is sucker-punched by A. This inequality is about B, but it also implies that A has a possible first-strike advantage as well.

Here’s what this means for the bargaining situation. A does not attack first over negotiating if \(1 - p_{(second)} - k \le 1 - x\), which is equivalent to \(x \le p_{(second)} + k\). This creates the following inequality.

Any offer of \(x\) that satisfies this inequality, should a value of \(x\) exist, induces negotiation over a first strike in a crisis bargaining situation where first strikes are now conceptually possible (i.e. explicitly modeled). This also means that \(p_{(first)} - k < p_{(second)} + k\) must hold for there to be negotiations. Equivalently:

Assume these values under these conditions. B’s probability of victory in war if it attacks first is .7 (i.e. \(p_{(first)} = .7\)) and its probability of victory in war if it attacks second (i.e. A attacks first) is .4 (i.e. \(p_{(second)} = .4\)). We’ll again hold \(k\) to be .1. This would be mean that \(p_{(first)} - k = .7 - .1 = .6\) and \(p_{(second)} + k = .4 + .1 = .5\).

The inequality \(p_{(first)} - k \le x \le p_{(second)} + k\) does not hold because .5 is not greater than .6. Alternatively, \(p_{(first)} - p_{(second)} < 2k\) is not true either because .2 is not greater than .3. In other words, first-strike advantages here are so large that they effectively eliminate the bargaining space. No negotiation is possible that can obviate this situation.

The second kind of commitment problem is comparably as ubiquitous. These are time-inconsistency problems. These too are broad and refer to any number of things, but one application here is a situation in which an actor exchanges a good now for a good to be given later. Consider the (stylized) case of the Israel-Palestine dispute, in which negotiators for years tried to seek a land for peace formula outlined in UN Security Council Resolution 242 after the Six-Day War. In other words, Israel would give up land to the Palestinians so that they may pursue self-determination. In exchange, the Palestinian Authority would disarm its more radical elements that wage violence against Israel. From the Israeli perspective, it gives up land now for peace to be given later. However, the Oslo accords happened as a provisional agreement with the idea of a more substantive agreement to be reached at Camp David in 2000. Thus, from one perspective, the concession of land to Palestine while negotiations were ongoing amounted to a concession from Israel (State A) to Palestine (State B) that changed Palestine’s probabilistic assessment of victory in conflict from \(p\) to \(p + \Delta\). Amid other ongoing issues at stake in the Camp David negotiations (e.g. Israel’s expanded settlements, Temple Mount, and more), Palestine could not credibly commit to controlling and disarming its radicals and the territorial concession gave it more resources that made it more powerful in 2000 than it was in 1993. The epilogue here was the Al-Aqsa Intifada after the failure to achieve a more lasting peace agreement. Time-inconsistency problems as a type of commitment problem pervade this issue to this day.

Conclusion

The hope is this primer amounts to a crash course on how to think about war for students who have not encountered Fearon’s (1995) seminal paper, or discussion of it, at the introductory level. War is bargaining failure. No matter the rarity of the event, it’s made possible by the presence of indivisible goods (in theory), uncertainty about the nature of the game (i.e. about probability of victory and the costs involved), and the inability to credibly commit to a peaceful resolution in an anarchic international system. My upper-division course uses this as background upon which to understand the basic correlates of war. Thus, the rationalist explanation for war framework emerges as the backdrop of the theoretical arguments about why territory is the most war-prone issue in international politics (i.e. it’s practically indivisible, if you want to use that language) or why alliances might be steps to war or paths to peace (i.e. they alter the probability of victory in war). Students can choose to dwell on the formal-theoretic mechanics of this—lots of people have!—but they do not need get too far into those weeds to understand the basic takeaway. The basic takeaway in turn is the foundation on which I try to get students to think about the study of international conflict.